Is The Sun Solid Liquid Or Gas?

Greetings, space enthusiasts and curious minds alike! Have you ever found yourself gazing up at the sun, that blazing orb in the sky, and wondered about its true nature? Is it solid, liquid, or gas? It’s a question that has fascinated humans for centuries, sparking the imaginations of poets, scientists, and dreamers across the ages.

The Sun is a medium-sized star at the center of the solar system and one of the hundreds of billions of stars in the Milky Way galaxy. It’s estimated to be about 4.6 billion years old, and its energy drives Earth’s climate and weather. The Sun also supports almost all life on Earth through photosynthesis, which plants and other organisms use to convert light energy captured from the Sun into chemical energy. It is a near-perfect sphere of scorching hot hydrogen and helium.

Communications on Earth scientists believe the Sun has enough nuclear fuel for another 5 billion years. After that, the Sun will begin to burn helium and expand a hundred times its current size, swallowing the Earth. It’s believed the red giant Sun will burn for another billion years and then collapse into a white dwarf about the size of Planet Earth. The state of the sun is still debated. It looks like a solid from the earth, liquid from a telescope, and gaseous or plasma form scientifically.

We’re going on a cosmic journey to answer this burning question. So, grab your sunglasses (figuratively speaking, of course), and let’s dive into the heart of our solar system to uncover the secrets of the sun’s composition. Prepare to illuminate your mind with the wonders of the universe!

Is the sun solid, liquid, or gas?

The sun is neither a solid nor a liquid. It’s gaseous and plasma! But there are a lot of arguments about the gaseous sun that can not be negligible. The body-centered cubic structure of the Sun’s core region comprises type 2 metallic hydrogen, a compress. Therefore, more metallic hexagonal planar structure.

Type 1 and type 2 metallic hydrogen can be viewed as a one-component plasma wherein the protons are restricted to their lattice points. The electrons are freely delocalized. In the liquid metallic hydrogen model of the Sun, no radiative zone has characterized the standard model. The Sun seems like a fully compressible ideal gap in the standard model. It has no surface since gases are not known for their surface-forming abilities.

• The sun is made of 91.0% hydrogen and 8.9% helium. By mass, it is about 70.6% hydrogen and 27.4% helium.

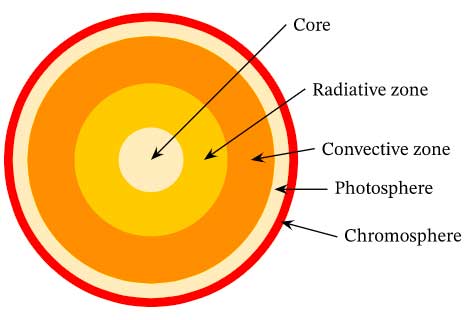
The sun has 5 main zones: core, radiative zone, convection zone, photosphere, and chromosphere.

Core

In this model, the central core of the Sun is believed to have a density approaching 150 grams per centimeter cube and reaches temperatures of 50 million Kelvin degrees. The density of the outer core is said to be about 20 grams per centimeter cubed. It is important to note that astronomers know from helioseismic studies that the Sun’s core undergoes solid-body rotations. Gases cannot rotate in that way.

The core is the region where nuclear reactions occur in the standard model. The Sun is limited to obtaining its vast majority of energy by directly converting hydrogen to helium. However, a small amount of helium arises through intermediates, including beryllium, boron, and lithium. In all these cases, though, the end product is helium.

The Sun cannot synthesize elements beyond the lightest, focusing only on the synthesis of helium. In this way, modern solar Theory has crippled Sun because it can’t make any heavy elements. These are the first-generation stars. Since the core is proposed to be a nuclear reaction, it emits light as gamma and X-rays, which are very high frequency. After gamma and x-rays are emitted by the solar core, they are believed to enter the radiative zone, where they are repeatedly scattered, absorbed, and re-emitted.

Radiative zone

The radiative zone extends from above the core to the next zone and is said to have a density of about 20 grams per centimeter cubed to 0.2 grams per centimeter cube. A temperature ranges from 7 million degrees to 2 million degrees Kelvin. After millions of years in this zone, the trap photons finally emerged. However, with their constant interaction with interstellar matter, their frequency is said to have slowly decreased, shifting from the X-ray range to the optical.

Convective zone

As photons progress toward the surface of the Sun, they pass through the convective zone. From helioseismic measurements, the convective zone begins about 200,000 kilometers below the solar surface. It is said to have a temperature of 2 million Kelvin degrees in the standard model. It is the region of the Sun where convection currents transport solar energy from the top of the radiative zone to the photosphere. Nests in between the radiative zone and the convective zone, we find the tackle line layer. Once again, based on helioseismology, this is known to be a region of high shear forces within the Sun.

The mere existence of a tack-aligned layer is sufficient evidence that the Sun’s body cannot be gaseous. Different star types differ from the Sun by the size and content of their core, radiative, and convective zones.

Photosphere

In the standard model, the photosphere has a temperature of about 5700 degrees Kelvin with an extremely low density of only two times 1e-7 grams per centimeter cubed. This density is lower than those made in a laboratory vacuum. Once photons cross the photosphere, they make their way into outer space.

Chromosphere

The chromosphere is around the photosphere, with the calculated density in the standard model of about 1e-12 grams per centimeter. The temperature will be slightly below the order of the photosphere. That density is one 100,000 of the density of the photosphere. Then comes the hypothesized transition zone. The outer solar atmosphere temperature rapidly increases from about 10,000 Kelvin degrees to nearly 1 million Kelvin degrees. The density of the outer atmosphere can drop to less than one million of the value of the level at the chromosphere.

Corona

According to modern theory, the temperature is thought to reach millions of degrees in the corona. Corona is known to be associated with the production of emission lines. Given rising to the corona in the standard model. It is interpreted as the result of the strange heating of the corona to millions of degrees. This increases temperature with elevation above the solar surface because gases can only produce emission lines via heating in this model. Still, that conjecture is not reasonable and violates thermodynamic laws.

The liquid metallic hydrogen model explains these emissions by invoking the high electron affinity of metallic hydrogen in the corona. When free atoms interact with this material, they are stripped of many electrons, resulting in a highly ionized species. This mechanism allows the corona to harvest electrons and maintain the electrical neutrality of the solar body.

Sun’s state explanation

The Sun is viewed as a fully compressible object in the standard model. Also, it is treated mathematically using the ideal gas law. This expression was first obtained by observing gases in containers.

Ideal gas law, PV = nRT

In this equation, P represents pressure, V is the volume, the number of particles expressing moles (n) is the gas constant, and T is the temperature. Fixing the number of moles and the temperature makes the right-side constant. In that case, increasing pressure will result in a decrease in volume.

While increasing volume decreases pressure. Now, the problem with utilizing the ideal gas law to treat the interior of a gaseous Sun is relatively easy to explain. How do we define pressure? It’s the amount of force applied to a given area. For instance, its units are often expressed as pounds per square inch or Newton’s per square meter.

Unfortunately, in the gaseous model of the Sun, there are no actual surfaces by which pressure can even be defined. There is no area in the force over the area definition of pressure, making the ideal gas law unusable. Astronomers use imaginary surfaces in their models to skirt around this problem. But as will be seen below, this is not a solution.

Homer Lane ignored this problem and applied the ideal gas law to the Sun in 1870. There are two problems if the Sun truly has an entirely gaseous interior.

• First, how do astronomers prevent the Sun from collapsing on itself?
• Secondly, how does a gaseous Sun maintain a stable radius?

Remember that the rule in the laboratory is that a gas expands to fill the void, yet the Sun is stable. So, how is that achieved if the Sun is truly a gas?

Astronomers solved the stability problem by invoking a principle called hydrostatic equilibrium. It constitutes a balance between gravity gas pressure and radiation pressure. The birth of the standard model begins by considering gravity. Most of us recognize that the Earth has more gravity than the moon. We have all seen movies of Apollo astronauts bouncing around while gazing at the Earth.

The Sun has a great mass of two times 10 to 30 kilograms. That’s more than 300,000 times the mass of the Earth. The Sun is also unbelievably big. Inside its volume, as defined by the photosphere, one could fit over 1 million Earths. Despite its huge mass and volume, it is interesting to highlight that our star has a very ordinary density of only 1.4 grams per centimeter cube. It is close to the density of water at 1 gram/centimeter cubed and about 1/4 of the density of the earth.

Given the Sun’s mass, it is not too much to believe that the service gravity of our star is nearly 30 times what we experience here on Earth. Astronomers argue that externally directed gas and radiation pressures counterbalance the inward-directed force of gravity within each star. When all these forces balance, we have hydrostatic equilibrium.

• For a start, the size of Sun theory suggests a gas pressure produced by electrons primarily acts to oppose the force of gravity. Within giant stars, however, radiation pressure becomes dominant.

What is gas pressure? First, think about the 5 layers of atmosphere above the Earth. Gas pressure supports the atmosphere. As you remember earlier, pressure is equal to force over an area. Gas pressure is generated when an atom in our atmosphere strikes the planet’s surface.

Much like a billiard ball, it bounces off the surface and is redirected upward. The net result is that any movement of an atom downward immediately transforms upward. To generate atmospheric gas pressure, we needed an actual surface. However, there is no surface in a standard model of the Sun!

LV Faye was the first to deprive the Sun of an actual surface when he argued in 1865 that it was only apparent. He could not do otherwise because he was promoting a gaseous solar body. Today, astronomers tell us that the surface of the Sun is nothing but an optical illusion. Given the theory that the Sun is a ball of gas, they had no choice.

The real fact about Sun

Gases can never have an actual surface. But if the Sun has no surface and its interior is entirely gaseous, how could it generate gas pressure? After all, the only surfaces inside a gaseous Sun are imaginary. Clayton uses an imaginary surface to argue that the Sun’s interior can support electron gas pressure. The problem, of course, is that imaginary surfaces are actual. Returning to the billiard table can give some insight into this question.

For example, suppose you have some balls, and each ball represents a gas particle. The bank of the table is an actual surface. The angle at which the cue ball strikes the bank will equal the angle at which it leaves. There can be a complete reversal of direction. But if the cue ball hits another ball, it will transfer momentum to the second ball and remain stationary after impact. This example makes it easy to say why particles within a gaseous Sun could never act as an actual surface.

Clayton’s imaginary surface cannot justify gas pressure in the Sun. When a particle moves downward towards an imaginary plane, it will not change direction upon reaching it. Imagine a particle on the Sun moving downward and hitting another particle.

It can simply push the second particle deeper into the solar body. This collision does result in a downward force, not an upward one. There can be a complete transfer of momentum with no change in direction. Conversely, the opposite can be argued if the particle initially moved upward. It is impossible to generate net gas pressure inside an object like a gaseous Sun. No surface, no pressure.

If one adds the force of gravity, gas-particle movements inside a gaseous Sun are more likely to generate solar collapse than a stable structure. Consequently, astronomers cannot justify electron gas pressure as a component of hydrostatic equilibrium within the Sun.

Then, we come to radiation pressure. The escape of a photon from the Sun’s center involves millions of years of bouncing around within the interior. Light moves at 3 times 10 to the 8th meters per second in a vacuum. That’s a lot of speed.

To place everything in perspective, the width of the entire Milky Way galaxy is 100,000 light-years. It is assuming a light speed in a vacuum. The standard model requires some light to travel ten times the galaxy’s diameter, of which the Sun is only a speck before escaping. But one of the biggest problems is invoking internal radiation in the first place.

Last words

Objects strive for internal thermal equilibrium on Earth using conduction and convection, not radiation. Radiative processes are reserved for reaching equilibrium with the outside world. Consequently, the standard Sun model suffers from two flaws.

• Gas pressure cannot exist without an actual surface, and there are none within a gaseous Sun.
• Objects on Earth do not use radiative processes to achieve internal thermal equilibrium.

Conduction and convection are reserved for this situation.

We’ve journeyed to the core of our solar system and back, unraveling the mysteries of the sun’s composition. Hopefully, this exploration has not only answered your burning question but also sparked a deeper fascination with the celestial forces that shape our universe.

The next time you feel the sun’s warmth on your face, there’s a whole world of incredible science and phenomena behind that comforting glow. Thank you for joining us on this enlightening expedition across the cosmos. Keep looking up, and stay curious—there’s always more to discover in the vast, beautiful expanse of space!

More Articles:

How Was The Sun Discovered?

What Would Happen If The Aun Vanished?

Is The Sun A Giant Ball Of Fire?

Does The Universe Expand Faster Than Light?